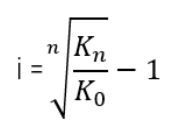Meine Kaffeemaschine wurde repariert. Der Techniker meinte, die Muffbrieme war verbrömmelt und angeeumelt. Man musste nur die Dichtbrumme abquastern und neue Flanschpaddendranwöhnern. Die sind nun vierfach gefröbbelt und neu umwienert. Na – das hätte ich auch selbst machen können.
Witzig. Vorlauter Formeln und Assistenten übersieht man manchmal die Wirklichkeit.
Wir schauen die Zielwertsuche an. Mit der Funktion RMZ (regelmäßige Zahlungen) wird die Annuität berechnet.
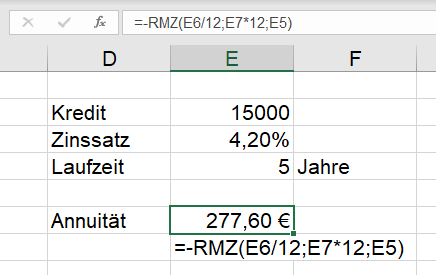
Nun soll „zurückgerechnet“ werden. Ich möchte wissen wie hoch der Zinssatz bei einer Rückzahlung von 220 Euro ist. Also Zielwertsuche (sie soll ja auch gezeigt werden:
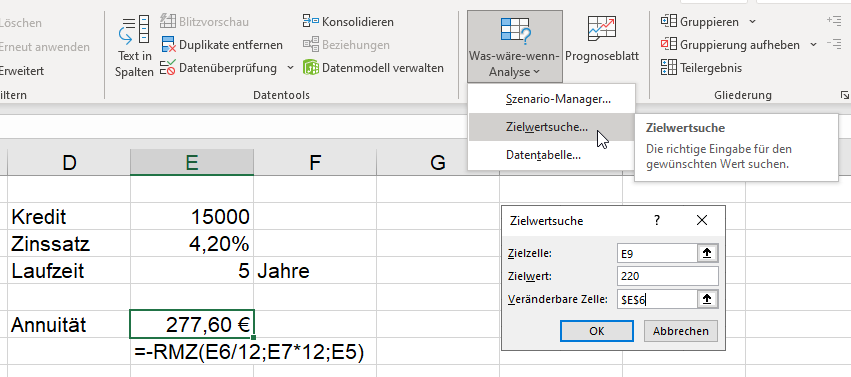
Sie rechnet und liefert:
-4,92% !?! Minus !?!
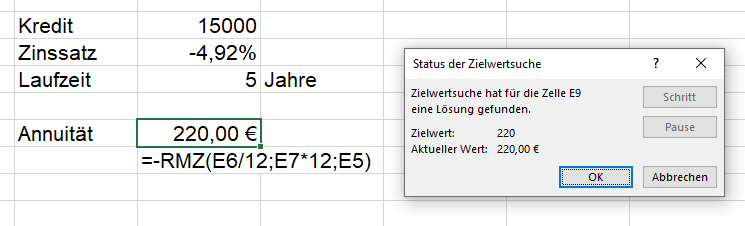
Es dauert eine Weile, bis wir verstehen: Das Ergebnis ist korrekt. Man müsste mit negativen Zinsen rechnen, um auf diesen Betrag zu kommen … Doch nicht falsch und auch nicht so unrealistisch.
Danke an Hartmut Hilbich für dieses Beispiel.