Die Küche sieht aus wie Sau. Hab das Licht ausgemacht. Jetzt geht’s.
Ich erstelle eine 3 x 3-Matrix.
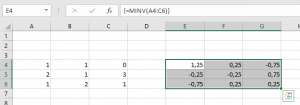
Berechne die inverse Matrix mit der Funktion MINV:
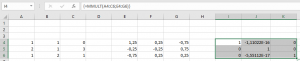
Multipliziere die beiden Matrizen mit der Funktion MMULT – das Ergebnis – na, ja: fast richtig. Ein bisschen Abweichung ist halt häufig in Excel:
Wenn ich die berechneten Zahle der inversen Matrix per Hand eingebe, erhalte ich eine korrekte Einheitsmatrix. Die Rechenungenauigkeit liegt also bei MINV.

Wenn man eine gewisse EXCEL-Unschärfe bei der Berechnung – wie dargestellt – in Kauf nimmt und z.B. eine Genauigkeit von 4 Nachkommastellen für die Probe, ob die Matrizenmultiplikation denn dann auch die Einheitenmatrix ergibt, in Kauf nimmt, kann man die MMULT-Formel auch mit der RUNDEN-Funktion umschliessen und erhält dann sogar eine „perfekte“ Einheitsmatrix:
={RUNDEN(MMULT(A4:C6;MINV(A4:C6));4)}
Übrigens sei der Hinweis erlaubt, dass man seit EXCEL 2013 auch Einheitsmatrizen simpel erzeugen kann (also weder über obigen Umweg noch per manueller Eingabe von Nullen und dann Befüllung der Hauptdiagonalen mit Einsen): Es gibt die Matrix Funktion MEINHEIT, in der man als Parameter noch die Zeilenanzahl der quadratischen Matrix angeben muss.
Ja, Matthias – das ist richtig – mit dem Matrixfunktionen kann man gut arbeiten, wenn man die Unschärfe in Kauf nimmt.
Und danke für den wertvollen Hinweis mit MEINHEIT – ich gestehe – ich habe diese Funktion übersehen … wahrscheinlich weil ich wenig Matrizenberechnungen durchführe.